Das Apollonische Problem
Das Apollonische Problem (Problem des Apollonios) ist eines der berühmtesten Probleme der antiken Geometrie.
Es geht darum, die Kreise zu konstruieren, die drei beliebige vorgegebene Kreise berühren.
Im folgenden wollen wir entartete Kreise ausschließen, also Kreise mit dem Raidius 0 oder unendlich.
Kreise mit Radius 0 wären Punkte und mit Radius unendlich Geraden.
Es gibt verschiedene Lösungsansätze, sowohl geometrische als auch analytische. Wie wollen einen
analytischen Ansatz machen. Wir legen auf die drei gegebenen Kreise drei neue Kreise, d.h. mit
identischen Mittelpunkten aber anderen Radien, so das deren Schnittpunkt der Mittelpunkt des Lösungskreises ist.
In manchen Fällen haben wir auch zwei Schnittpunkte, dann wenn sich nämlich alle drei Kreise in zwei Punkten
schneiden.
Dann haben wir also zwei Lösungskreise.
Die Überlegung zu diesem Ansatz soll die folgende Grafik veranschaulichen:
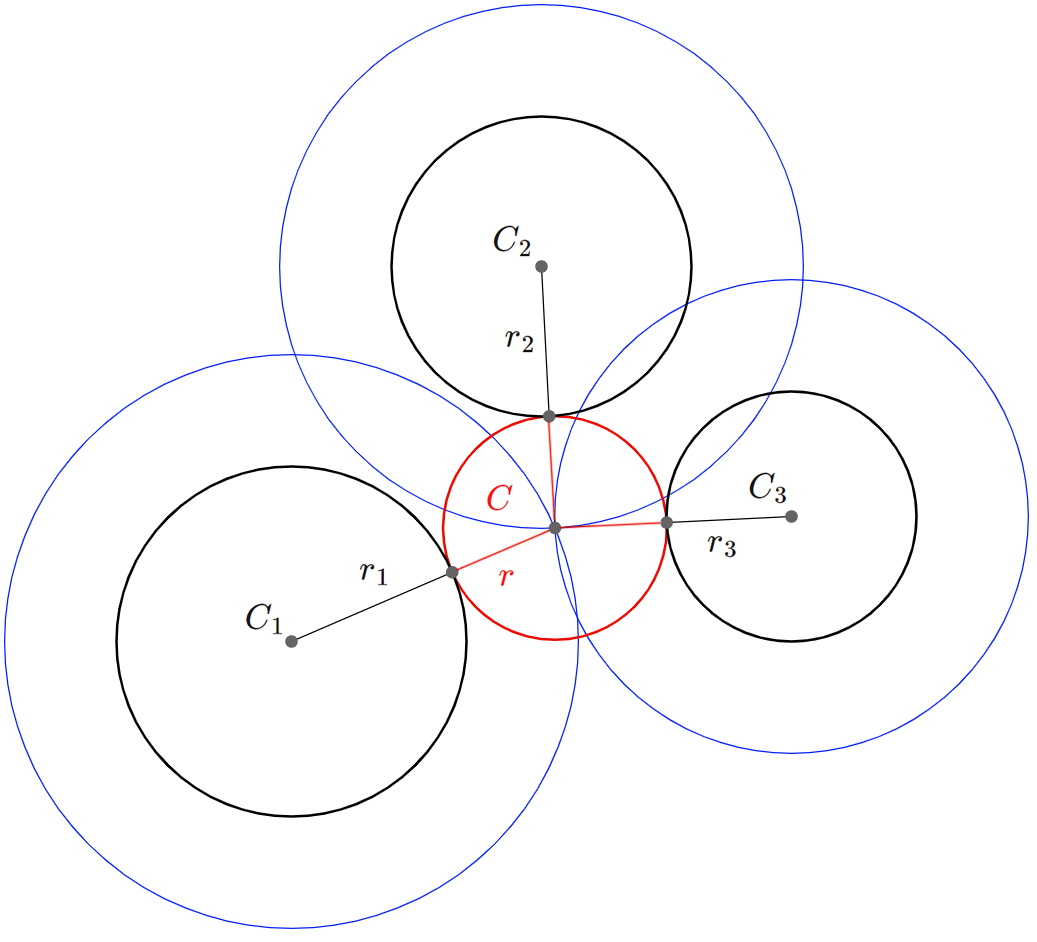
Hier ist nur 1 von 8 Lösungskreisen abgebildet. Und zwar die Lösung, wo der Lösungskreis alle 3 gegebenen Kreise von außen berührt. Der Ansatz für diese Lösung ist: $$(I_+)\quad(x-x_1)^2+(y-y_1)^2=(r+r_1)^2$$ $$(II_+)\quad(x-x_2)^2+(y-y_2)^2=(r+r_2)^2$$ $$(III_+)\quad(x-x_3)^2+(y-y_3)^2=(r+r_3)^2$$ Möchten wir, dass der Lösungskreis die 3 gegebenen Kreise von innen berührt, müssen wir folgenden Ansatz machen: $$(I_-)\quad(x-x_1)^2+(y-y_1)^2=(r-r_1)^2$$ $$(II_-)\quad(x-x_2)^2+(y-y_2)^2=(r-r_2)^2$$ $$(III_-)\quad(x-x_3)^2+(y-y_3)^2=(r-r_3)^2$$ Die nächste Abbidlung veranschaulicht diesen Ansatz:
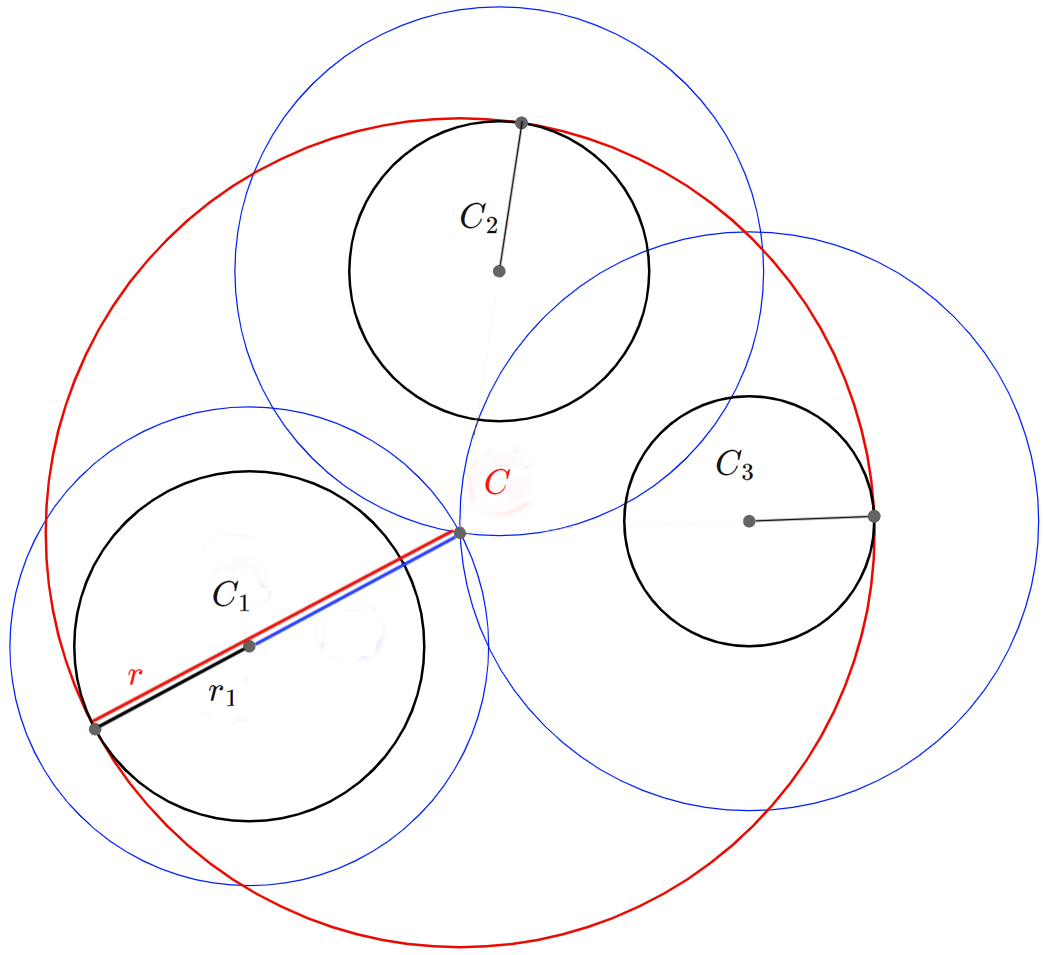
Beim Lösen des Gleichungssytems ergibt sich, wie wir später sehen werden, eine quadratische Gleichung für den Radius $r$. In manchen Situation ergeben sich also 2 Lösungen für der Radius $r$ (für ein Gleichungssystem). Im folgenden ist eine Lösung für den Fall, und zwar wo die 2 Lösungskreise die gegebenen 3 Kreise von außen berühren, abgebildet.
Der allgemeine Ansatz lautet also:
$$(I)\quad(x-x_1)^2+(y-y_1)^2=(r \pm r_1)^2$$ $$(II)\quad(x-x_2)^2+(y-y_2)^2=(r \pm r_2)^2$$ $$(III)\quad(x-x_3)^2+(y-y_3)^2=(r \pm r_3)^2$$
$(I)$,$(II)$ und $(III)$ ausmultipliziern ergibt:
$$(I_1) \quad x^2-2xx_1+x_1^2+y^2-2yy_1+y_1^2=r_1^2+2(\pm r_1)r+r^2$$
$$(II_2) \quad x^2-2xx_2+x_2^2+y^2-2yy_2+y_2^2=r_2^2+2(\pm r_2)r+r^2$$
$$(III_3) \quad x^2-2xx_3+x_3^2+y^2-2yy_3+y_3^2=r_3^2+2(\pm r_3)r+r^2$$
$(I_1)-(II_2)$ und $(I_1)-(III_3)$ ergibt sortiert:
$$2(x_1-x_2)x+2(y_1-y_2)y+2(\pm r_1-(\pm r_2))=(x_1^2+y_1^2-r_1^2)-(x_2^2+y_2^2-r_2^2)$$
$$2(x_1-x_3)x+2(y_1-y_3)y+2(\pm r_1-(\pm r_3))=(x_1^2+y_1^2-r_1^2)-(x_3^2+y_3^2-r_3^2)$$
mit:
$$a_1=2(x_1-x_2)$$
$$b_1=2(y_1-y_2)$$
$$c_1=2(\pm r_1-\pm r_2)$$
$$d_1=(x_1^2+y_1^2-r_1^2)-(x_2^2+y_2^2-r_2^2)$$
$$a_2=2(x_1-x_3)$$
$$b_2=2(y_1-y_3)$$
$$c_2=2(\pm r_1-\pm r_3)$$
$$d_2=(x_1^2+y_1^2-r_1^2)-(x_2^2+y_2^2-r_2^2)$$
erhalten wir ein LGS mit zwei Gleichungen:
$$(I_a) \quad a_1x+b_1y+c_1r = d_1$$
$$(I_b) \quad a_2x+b_2y+c_2r = d_2$$
Wir lösen das LGS zuerst für y($r$ soll als konstant betrachtet werden):
Dazu multipliziern wir die erste Gleichung mit $a_2$ und die zweite mit $a_1$
$$\quad a_1x+b_1y+c_1r = d_1 \quad |\cdot a_2$$
$$\quad a_2x+b_2y+c_2r = d_2 \quad |\cdot a_1$$
Wir erhalten:
$$\quad a_1 a_2 x + a_2 b_1 y + a_2 c_1 r = a_2 d_1$$
$$\quad a_1 a_2 x + a_1 b_2 y + a_1 c_2 r = a_1 d_2$$
Jetzt ziehen wir die erste von der zweiten Gleichung ab und somit eleminieren wir $x$.
$$\underbrace{(a_1 b_2 - a_2 b_1)}_{=:k}y + \underbrace{( a_1 c_2 - a_2 c_1 )}_{=:-s_2} r = \underbrace{(a_1 d_2 - a_2 d_1)}_{=:m_2}$$
$$(K_y) \quad ky-s_2 r = m_2$$
$$\leftrightarrow y=\underbrace{\frac{m_2}{k}}_{=:C}+\underbrace{\frac{s_2}{k}}_{=:D}r$$
Man gehe analog mit $x$ vor und erhält:
$$\quad a_1 b_2 x + b_1 b_2 y + b_2 c_1 r = b_2 d_1$$
$$\quad a_2 b_1 x + b_1 b_2 y + b_1 c_2 r = b_1 d_2$$
Jetzt ziehen wir die zweite von der ersten Gleichung ab und somit eleminieren wir $y$.
$$\underbrace{(a_1 b_2 - a_2 b_1)}_{=:k}x + \underbrace{( b_2 c_1 - b_1 c_2 )}_{=:-s_1} r = \underbrace{(b_2 d_1 - b_1 d_2)}_{=:m_1}$$
$$(K_x) \quad kx-s_1 r = m_1$$
$$\leftrightarrow x=\underbrace{\frac{m_1}{k}}_{=:A}+\underbrace{\frac{s_1}{k}}_{=:B}r$$
Wir fassen zusammen: $$(I_x) \quad x=A+Br$$ $$(I_y) \quad y=C+Dr$$ mit: $$k:=a_1b_2-a_2b_1$$ $$m_1:=b_2d_1-b_1d_2$$ $$s_1:=b_1c_2-b_2c_1$$ $$m_2:=a_1d_2-a_2d_1$$ $$s_2:=a_2c_1-a_1c_2$$ wobei ($k\neq 0$): $$A:=\frac{m_1}{k}$$ $$B:=\frac{s_1}{k}$$ $$C:=\frac{m_2}{k}$$ $$D:=\frac{s_2}{k}$$ $$E:=A-x_1$$ $$F:=C-y_1$$
Wir setzen $x$ und $y$ in (I) ein und lösen nach $r$ auf:
$$(A+Br-x_1)^2+(C+Dr-y_1)^2=(r\pm r_1)^2$$
mit $E=A-x_1$ und $F=C-y_1$ reduziert sich die Gleichung zu:
$$(E+Br)^2+(F+Dr)^2=(r\pm r_1)^2$$
Ausmultiplizieren:
$$\leftrightarrow \quad E^2+2EBr+B^2r^2+F^2+2FDr+D^2r^2=r^2\pm 2rr_1 +r_1^2$$
Sortieren:
$$(\underbrace{B^2+D^2-1}_{\alpha})r^2+(\underbrace{2(EB+FD-(\pm r_1))}_{\beta})r+\underbrace{F^2+E^2-r_1^2}_{\gamma}=0$$
Wir fassen zusammen und erhalten eine quadratische Gleichung mit der Unbekannten $r$.
$$\alpha r^2 + \beta r + \gamma = 0$$
mit:
$$\alpha=B^2+D^2-1$$
$$\beta=2(EB+FD-(\pm r_1))$$
$$\gamma=F^2+E^2-r_1^2$$
Man löse die quadratische Gleichung und erhalte je nach Situation eine oder zwei Lösungen für den Radius.
Die negativen Lösungen fallen weg, da es keine negativen Radien geben kann. Den/die Radius/Radien $r_1$ oder/und
$r_2$
in $(I_x)$ und $(I_y)$ einsetzen ergibt die Koordinaten des Mittelpunktes der/des Lösungskreise/s.
Wenn man alle Kombinationen durchrechnet muss man 8x die quadratische Gleichung lösen. Es ergeben sich
aber trozdem maximal 8 und nicht 16 Lösungen, da etweder, je nach Situation, die Diskriminante 0 wird, negative
Lösungen
wegfallen oder identische Lösungen auftreten.
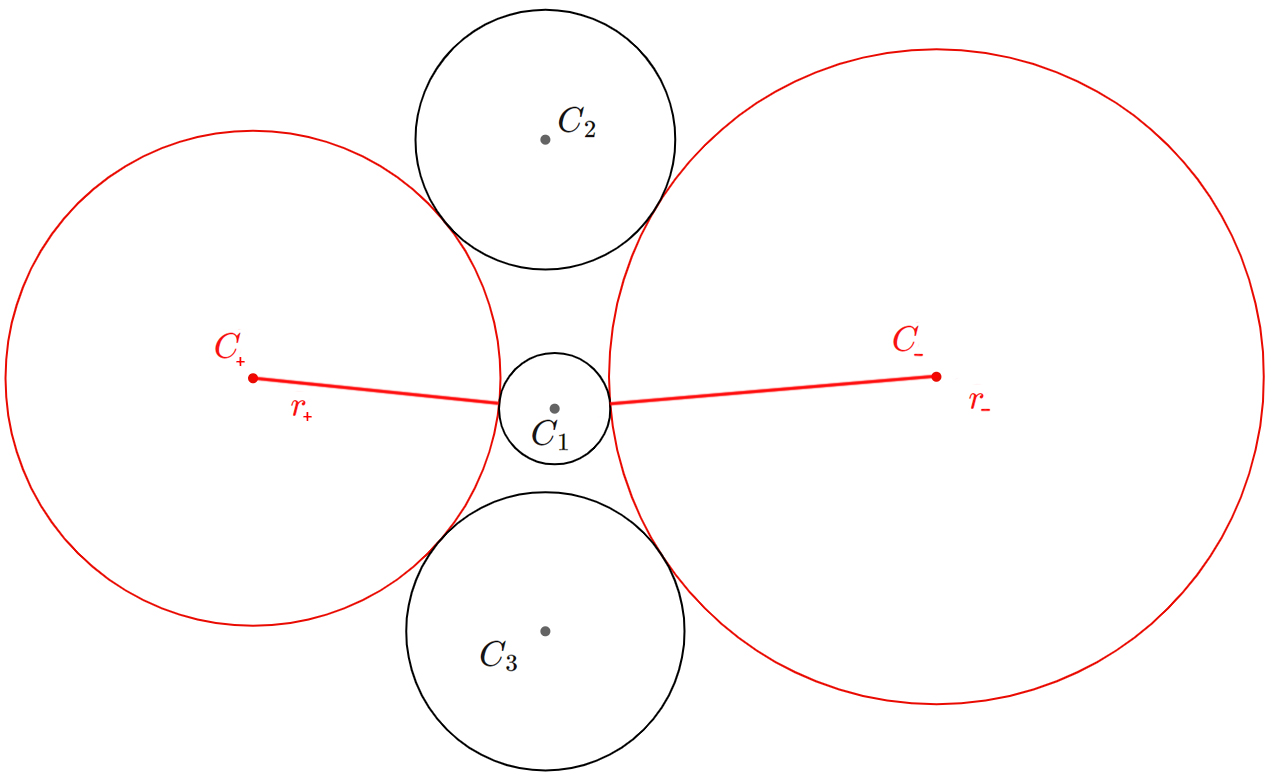
Wenn der Fall $k=0 \land (s_1\neq 0 \lor s_2\neq 0)$ eintritt, dann liegen alle Mittelpunkte
der gegebenen Kreise auf einer Linie, und wir haben 2 Lösungen die symmetrisch sind. Also
einen Radius $r$ für die Lösungskreise. Folgende Rechnung muss jetzt durch geführt werden:
Wir betrachteten nochmal die Gleichungen $(K_x)$ und $(K_y)$ von oben:
$$(K_x) \quad kx-s_1 r = m_1$$
$$(K_y) \quad ky-s_2 r = m_2$$
Wir setzen $k:=0$ und lösen nach $r$ auf:
$$r=\frac{-m_1}{s_1}$$
falls $s_1 \neq 0$. Ansonsten:
$$r=\frac{-m_2}{s_2}$$
(Es muss wegen der Bedingung oben jetzt $s_2 \neq 0$ gelten (Warum? Gute Denkübung)).
Den gefundenen Radius $r$ in $(I)$ und $(I_a)$ eingesetzt ergibt ein
Gleichungssystem mit 2 Unbekannten und 2 Gleichungen. Hier nochmal die 2 Gleichungen von oben:
$$(I) \quad (x-x_1)^2+(y-y_1)^2=(\pm r_1+r)^2$$
$$(I_a) \quad a_1x+b_1y+c_1r = d_1$$
D.h. wir haben eine Kreisgleichung und eine Geradengleichung.
Geometrisch suchen wir also die Schnittpunkte von Kreis und Gerade.
Wir lösen $(I_a)$ zuerst nach $y$ auf:
$$y=\frac{d_1 - a_1 x - c_1 r}{b_1}=\underbrace{\frac{d_1-c_1 r}{b_1}}_{:=f}-\underbrace{\frac{a_1}{b_1}}_{=:g}x$$
$$y=f+gx$$
Wir setzen jetzt $y$ in $(I)$ ein und multipliziern aus:
$$x^2-2x_1 x + x_1^2 + (f+gx)^2 - 2(f+gx)y_1+y_1^2=r_1^2\pm 2r_1 r + r^2$$
Sortieren und zusammenfassen!:
$$\underbrace{(1+g^2)}_{=:a} x^2 + \underbrace{2(fg-y_1g-x_1)}_{=:b}x+\underbrace{f^2-2fy_1+x_1^2+y_1^2-r_1^2-(\pm 2 r_1r)-r^2}_{=:c} = 0$$
Diese Gleichung kann man mit der abc-Formel lösen. Man erhält entweder 0,1 oder 2 Lösungen.
Also keine, einen oder zwei Schnittpunkte. Die gefundene Lösung also das $x$ bzw. $x_1$ und $x_2$ in die obige
Gleichung $y=f+gx$ einsetzen und damit $y$ bzw. $y_1$ und $y_2$ ausrechnen.
Zur Erinnerung: Die Schnittpunkte sind die Mittelpunkte der Lösungskreise. Den Radius haben wir ja schon
vorher ausgerechnet(Es gibt nur einen Radius, da wir hier den symmetrischen Fall betrachten).
Wenn $a_1=0$, dann liegen alle 3 gegebenen Kreisen auf einer Vertikalen. Wenn $b_1=0$, dann auf einer Horizontalen(für $k\neq 0$).
Wenn sowohl $a_1=0$ also auch $b_1=0$, dann haben mindestens 2 der gegebenen Kreise den selben Mittelpunkt.
Für $a_1=0$ oder $b_1=0$ vereinfacht sich die Gleichung $(I_a)$ und man muss dementsprechend das Gleichungssystem lösen.
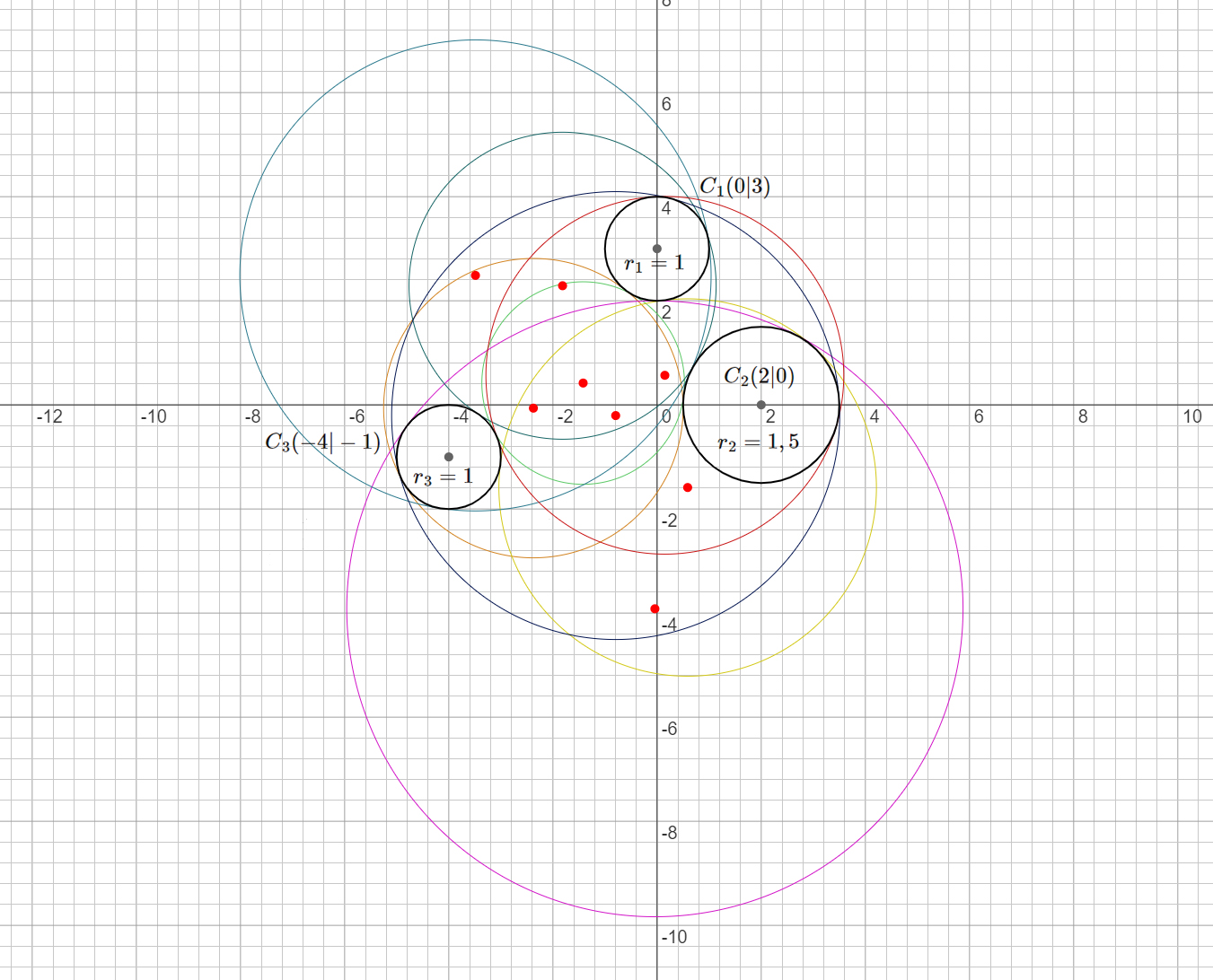
Zum Abschluss folgt eine Abbildung zur Komplettlösungen für den Fall $C_1(0|3)$ mit $r_1=1$, $C_2(2|0)$ mit $r_2=1,5$ und $C_3(-4|-1)$ mit $r_3=1.$