Meine Entdeckungen mit Hilfe der komplexen Zahlen in der Gaußschen Zahlenebene

Es ist sehr schwer geworden in der Mathematik noch etwas Neues zu entdecken!

Hier beschreibe ich einige meiner Entdeckungen mit Hilfe der komplexen Zahlen in der Gaußschen Zahlenebene!

Die gerade Linie der Planimetrie ist nichts anderes als eine geometrische Interpretation der unendlichen Zahlen. Daher auch der Begriff der Zahlengerade! Leider ist das nicht die Abbildung der Wirklichkeit des Alls oder eines zweidimensionalen Schnitts des Raums, denn in der physikalischen Realität existiert nichts Unendliches!

Wie sagte der Albert so schön: Es gibt nur zwei Unendlichkeiten!

1. Die Dummheit der Menschen
2. Das Weltall

Aber ob das unendlich ist, da sei er sich nicht so sicher (ist es ganz sicher nicht – wie er weiß!)

Allerdings lehrt man in allen Schulen bis heute ausschließlich nur die euklidische Geometrie: Wenn man zwei Geraden im Ursprung senkrecht aufeinander stellt, spricht man von einem kartesischen Koordinatensystem oder einer Ebene, die jedem Punkt eine Ordinate und eine Abszisse (Ko-Ordinate) zuordnet und umgekehrt. Diese kann man einfacher mit einer einzigen Zahl, nämlich komplex beschreiben. Aber obwohl komplexe Zahlen die ultimativ letzte allerdings unersetzlich z.B. bei der Beschreibung von Wellen oder Ψ-(psi-)-Wellen in der Quantenmechanik, welche die sowieso komplexe Schrödingergleichung erfüllen. Die komplexen Zahlen sind zweidimensional und eignen sich daher hervorragend zur Beschreibung der zweidimensionalen Ebene!

Die reelle Zahlengerade liefert die x-Achse. Eine Multiplikation mit der imaginären Einheit $i = \sqrt{-1}$ ist immer eine Drehung um 90º um den Ursprung im mathematisch positiven Sinn (= entgegen dem Uhrzeigersinn) und wir erhalten die imaginäre Achse als y-Achse.

Somit besteht eine umkehrbar eindeutige Beziehung zwischen den Punkten und den komplexen Zahlen. Die Darstellung von Geraden mittels einer komplexen Geradengleichung geschieht nun natürlich nicht mehr mit den beiden Variablen x und y, sondern durch eine Variable $z = x+iy$ und ihr konjugiert komplexes (hier immer mit einem Asterix gekennzeichnet)

$$z^*=x-iy$$

Die Addition von $z$ und $z^*$ liefert den doppelten Realteil, nämlich $2x$. $$x = \frac{1}{2}(z+z^*)$$ Und die Differenz von $z$ und $z^*$ ergibt den doppelten Imaginärteil $2yi$. $$y = \frac{z-z^*}{2i} = -\frac{1}{2}(z-z^*)i$$ da ja $i^2=-1$. ist

Interessanterweise lassen sich nun damit die exakten Koordinaten von Schnittpunkten oder Kreismittelpunkten berechnen!

Kennen wir eine Gleichung, in der nur Kreiskrümmungen vorkommen, dann erhalten wir eine Gleichung mit deren Kreiszentren ganz einfach, indem wir hinter jeder Krümmung mit dem entsprechenden komplexen Kreiszentrum $z$ multiplizieren. Das ist erstaunlich, und man kann die Kreiszentren berechnen!

Die Krümmung $\kappa$ eines Kreises ist der Kehrwert seines Radius

$$\kappa=\frac{1}{r}$$

Deshalb haben Geraden die Krümmung Null, denn es sind Kreise mit unendlich großem Radius! Und Punkte haben einen verschwindenden Radius, und haben daher eine unendliche Krümmung, denn sie sind unendlich krumme Kreise!!

Jede Gleichung aus nur Krümmungen kann man komplex erweitern, indem man jede Krümmung mit jeweils dem entsprechenden Kreismittelpunkt multipliziert, der komplex beschrieben wird!

Für die Summe der drei Ankreiskrümmungen $\kappa_a+\kappa_b+\kappa_c$ gilt, dass sie gleich der Krümmung $\frac{1}{r}$ des Inkreises ist!

$$\kappa_a+\kappa_b+\kappa_c=\kappa$$

wobei $\kappa = 1/r$ und $r$ der Inkreisradius ist. (Ankreise heißen engl. „excenter“, denn sie liegen immer außerhalb des Dreiecks)

Die Ankreiskrümmungen sind nämlich $x/A$, $y/A$ und $z/A$, wobei $x$, $y$ und $z$ die Tangentialabschnitte sind, für die die Summe je zweier eine Dreiecksseitenlänge ist und daher

$$\frac{x}{A}+\frac{y}{A}+\frac{z}{A}=\frac{u}{2A}=\frac{1}{r}$$

Sind die alle Seiten von außen berührenden drei Ankreisradien $r_a$, $r_b$ und $r_c$, dann gilt also

$$\kappa_a+\kappa_b+\kappa_c = \kappa_{Inkreis}$$

oder anders mit den Radien formuliert

$$\frac{1}{r_a}+\frac{1}{r_b}+\frac{1}{r_c} = \frac{1}{r}$$

Interessant ist nun, dass auch die Komplexifizierung mit den Kreis-Zentren als Faktoren

$$Z_a K_a + Z_b K_b + Z_c K_c = Z_{M_{Inkreis}} K_{Inkreis}$$

oder

$$\frac{Z_a}{r_a}+\frac{Z_a}{r_a}+\frac{Z_a}{r_a} = \frac{Z_{M_{Inkreis}}}{r}$$

richtig ist!

$z_i$ (für $i = a,b,c$) sind die Ankreiszentren (komplex geschrieben)

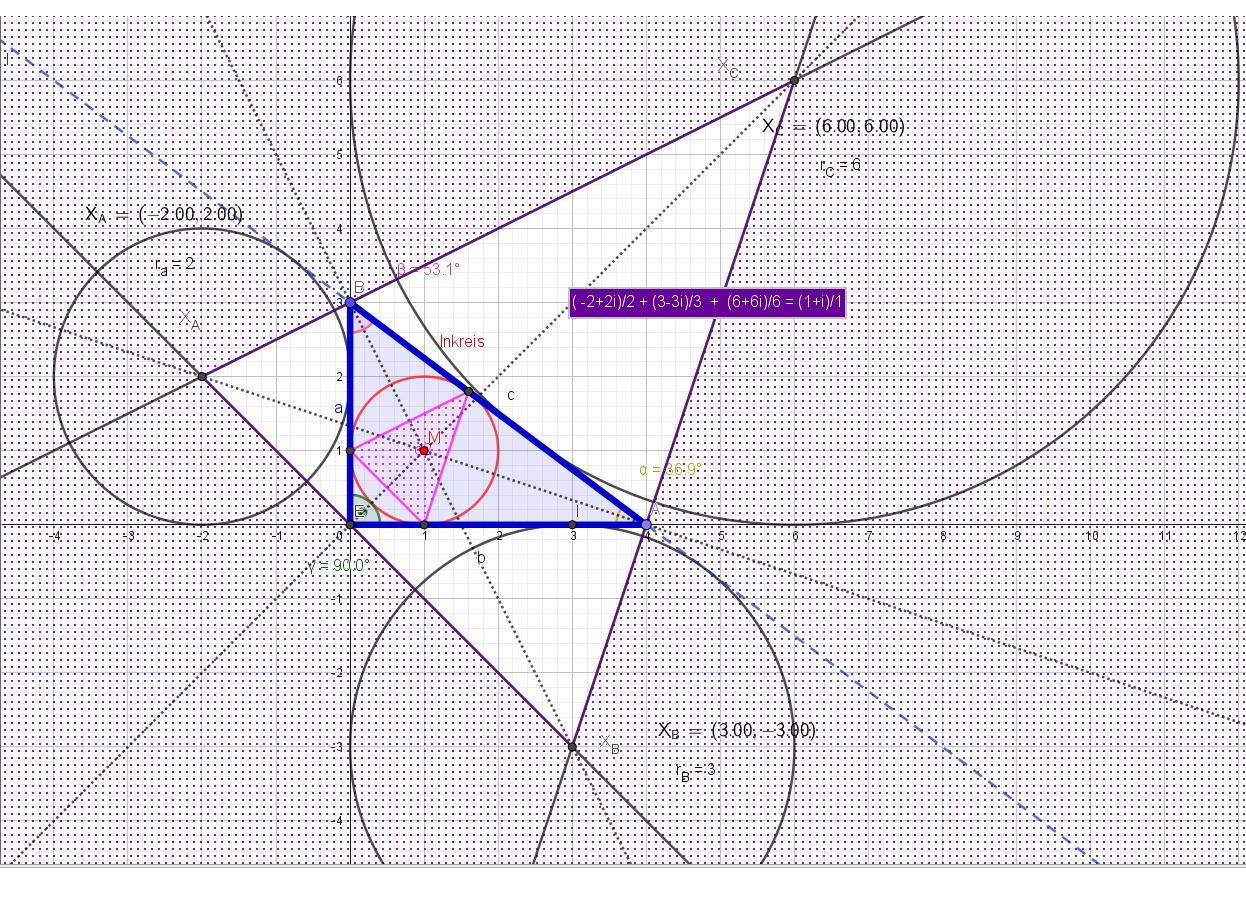
Betrachten wir ein einfaches Beispiel: Das kleinste natürliche Dreieck mit ganzzahligen Seitenlängen und Inhalt. Seitenlängen: $3$, $4$, $5$. Flächeninhalt: $6$. $A=4$, $B = 3i$ und $C = 0+0i = 0$ $$\frac{Z_a}{r_a}+\frac{Z_b}{r_b}+\frac{Z_c}{r_c} = \frac{Z_{M_{Inkreis}}}{r}$$

$Z_A = -2 + 2i, \quad r_a = 2$.

$Z_B = 3 - 3i, \quad r_b = 3$.

$Z_C = 6 + 6i, \quad r_c = 6$.

$$\frac{-2+2i}{2}+\frac{3-3i}{3}+\frac{6+6i}{6} = \frac{1+i}{1}$$

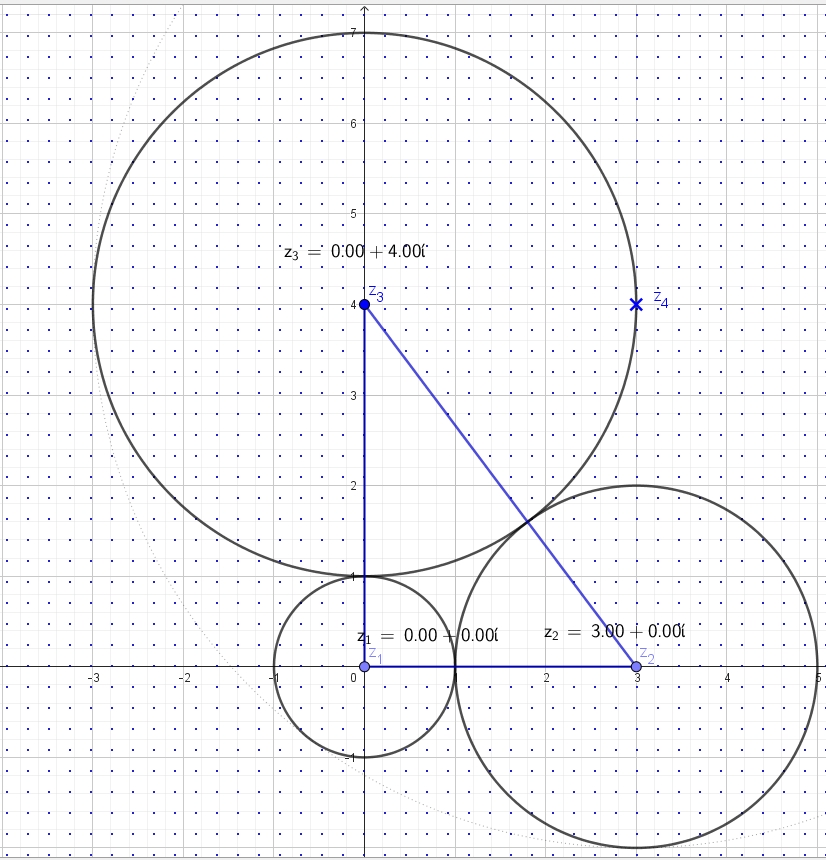
Wenn drei Kreise sich gegenseitig berühren, dann gibt es einen vierten (inneren oder äußeren) Kreis, der alle diese drei Kreise berührt.

Als einfaches Beispiel seien die drei Kreise

1. Der Einheitskreis um den Ursprung mit Mitte $z_1=0$ und Radius $r_1=1$
2. Der Kreis um den Punkt 3 auf der x-Achse $z_2=3$ und dem Radius $r_2=2$
3. Der Kreis um den Punkt 4 auf der y-Achse $z_3=4i$ und dem Radius $r_3=3$

Für die Krümmung des vierten Kreises $\boldsymbol{\kappa_4 = \frac{1}{r_4}}$ gibt es zur Berechnung die folgende Formel: $$\boldsymbol{\kappa_4=\kappa_1+\kappa_2+\kappa_3\pm 2 \sqrt{\kappa_1\kappa_2+\kappa_1\kappa_3+\kappa_2\kappa_3}}$$ (vergleiche Arno Fehringer >>Die Unbekannte Formel von Descartes<<)

In unserem Beispiel hat der vierte Kreis die Krümmung $$\boldsymbol{\kappa_4}=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}\pm 2\sqrt{1\cdot\frac{1}{2}+1\cdot\frac{1}{3}+\frac{1}{2}\cdot\frac{1}{3}}$$ $$=1+\frac{5}{6}\pm 2\sqrt{\frac{1}{2}+\frac{1}{3}+\frac{1}{6}}=\frac{11}{6}\pm 2\sqrt{1}$$ $$=\frac{11}{6}+2=\boldsymbol{\frac{23}{6}}$$ Der von innen alle drei Kreise mit den Radien $1$, $2$ und $3$ berührende Kreis hat also den (kleinen) Radius $r_4=\frac{6}{23}$ ($\to$ Abbildung 1)

(der zweite Wert liefert den äußeren Berührkreis mit dem Radius $r_4 = -6$ und der Mitte $3+4i$)

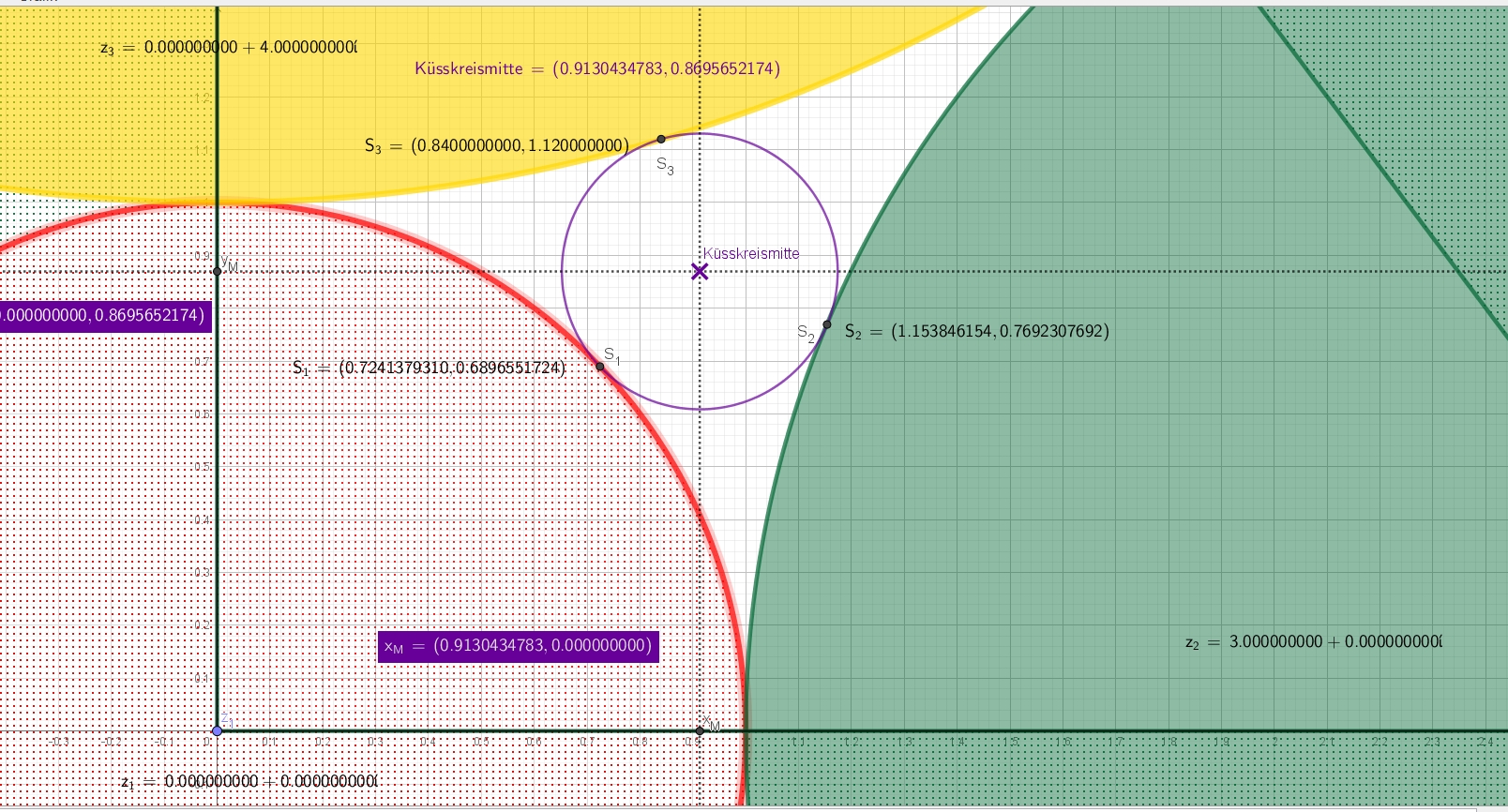
Aber wo ist das Zentrum von diesem inneren Berühr-Kreis?
Dafür komplexifizieren wir diese Formel, indem wir jede Krümmung mit seinem zugehörigen (komplex geschriebenen) Kreiszentrum multiplizieren, also jedes $\boldsymbol{\kappa_1}$ mit $z_1$, $\boldsymbol{\kappa_2}$ mit $z_2$ und $\boldsymbol{\kappa_3}$ mit $z_3$ $$\kappa_4 \boldsymbol{z_4}=\kappa_1\ \boldsymbol{z_1} + \kappa_2\ \boldsymbol{z_2} +\kappa_3\ \boldsymbol{z_3} \pm 2 \sqrt{\kappa_1\kappa_2 \boldsymbol{z_1}\boldsymbol{z_2}+\kappa_1\kappa_3\boldsymbol{z_1}\boldsymbol{z_3}+\kappa_2\kappa_3\boldsymbol{z_2}\boldsymbol{z_3}}$$ In unserem Fall wird wegen $\boldsymbol{z_1}=0$ die WURZEL einfacher zu $\sqrt{\kappa_2 \boldsymbol{z_2} \kappa_3 \boldsymbol{z_3}}$ $$\kappa_4 \boldsymbol{z_4}=1\cdot 0+\kappa_2\boldsymbol{z_2}+\kappa_3\boldsymbol{z_3}\pm 2 \sqrt{\kappa_2\kappa_3\boldsymbol{z_2}\boldsymbol{z_3}}$$ also $$\kappa_4 \boldsymbol{z_4}=\frac{1}{2}\cdot \boldsymbol{3}+\frac{1}{3}\cdot \boldsymbol{4i} \pm 2 \sqrt{\frac{1}{2}\cdot \boldsymbol{3} \cdot \frac{1}{3} \cdot \boldsymbol{4i}}$$ $$=1,5 + \frac{4}{3}\boldsymbol{i} + 2 \sqrt{2\boldsymbol{i}}$$ Da nun die Wurzel aus $\boldsymbol{i}$ gerade das $\frac{1}{\sqrt{2}}=\frac{1}{2}\sqrt{2}$ fache von $(1+\boldsymbol{i})$ ist, wird $\kappa_4 \boldsymbol{z_4} =1,5 + \frac{4}{3} \boldsymbol{i} + 2(1+\boldsymbol{i})= 3,5 + 3,33333…\boldsymbol{i}$ mit dem schon berechneten $\boldsymbol{\kappa_4} =\frac{23}{6}$ können wir den Mittelpunkt $\boldsymbol{z_4}$ berechnen, indem wir mit $6$ multiplizieren und durch $23$ dividieren: $$\boldsymbol{z_4} = (3,5 + 3,33333…\boldsymbol{i})\cdot \frac{6}{23}$$ $$= \frac{21}{23} + \frac{20}{23} \boldsymbol{i}$$ Der gesuchte Mittelpunkt ist $\boldsymbol{(0.9130434783…; 0.8695652174…)}$

Die komplexe Dreiecksgeometrie eignet sich hervorragend zur Berechnung der besonderen Punkte oder von Punkt-Entfernungen im Dreieck. Als möglichst einfaches Beispiel betrachten wir nur rechtwinklige Dreiecke mit $C=(0; 0)$, $A=(a; 0)$ und $B=(0; b)$ ( z.B. $a=3$ und $b=4$ )

Das Inkreiszentrum ist nun $$\boldsymbol{M}_i = r + \boldsymbol{i}r$$ d.h. hat die Koordinaten $(r; r)$ und die Inkreismitte bildet mit der rechten Ecke $C$ ein Quadrat! Den Inkreisradius erhalten wir mit $r = \frac{1}{2}(a+b-c)$, was in der obigen Abbildung $r = 1$ ist.

Allgemein für jedes beliebige Dreieck ist das Inkreiszentrum (für die Seitenlängen $a$, $b$ und $c$ mit $u=∑a_i = a+b+c$) $$\boldsymbol{M}_i = \frac{(a\boldsymbol{A}+b\boldsymbol{B}+c\boldsymbol{C})}{u}$$ d.h. es sind die mit der Seitensumme u gemittelten SeitenEckenProdukte: die x-Koordinate ist $$\boldsymbol{M}_x = (a\boldsymbol{A}_x+b\boldsymbol{B}_x+c\boldsymbol{C}_x)/u$$ und die y-Koordinate ist $$\boldsymbol{M}_y = (a\boldsymbol{A}_y+b\boldsymbol{B}_y+c\boldsymbol{C}_y)/u$$ Jeder besondere Punkt des Dreiecks ist eine Funktion der drei Eckpunkte $A$, $B$ und $C$. Viele besonderen Punkte (wie die Umkreismitte) sind allerdings etwas schwieriger! Einige einfache Beispiele seien nur kurz erwähnt: Der Seitenmittenkreis ist der Umkreis des Mittendeiecks (= Dreieck der Seitenmitten) Das Zentrum des Seitenmittenkreises (Feuerbach) ist allgemein die Mitte von $HM_u$ $$\boldsymbol{M}_u= \frac{1}{2}(\boldsymbol{A}+\boldsymbol{B})$$ (der Höhenschnitt H ist im Ursprung an der echten Ecke C).

Das Umkreiszentrum des Mittendreiecks $\boldsymbol{M}_F$ ist nun $$\boldsymbol{M}_F = \frac{1}{4}(\boldsymbol{A}+\boldsymbol{B})$$ ($C$ ist Ursprung) während der Schwerpunkt $\boldsymbol{S}=\frac{1}{3}(\boldsymbol{A}+\boldsymbol{B})$ ist.

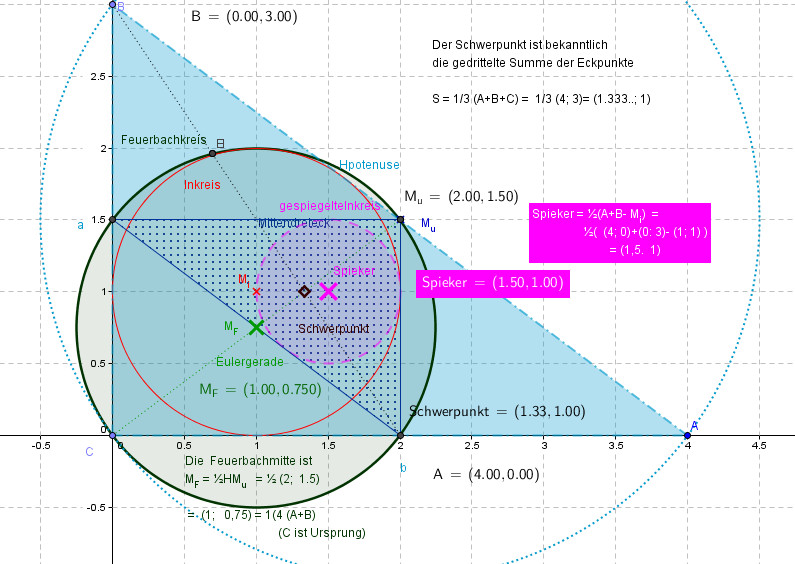
Der Spiekerkreis ist der Inkreis des Mittendreiecks Es ist der zentrisch am Schwerpunkt $S=\frac{(\boldsymbol{A}+\boldsymbol{B})}{3}$ gestreckte Inkreis mit dem Steckungsfaktor $k = -\frac{1}{2}$ $$Spieker = \frac{1}{2}(\boldsymbol{A}+\boldsymbol{B} – \boldsymbol{M}_i)$$

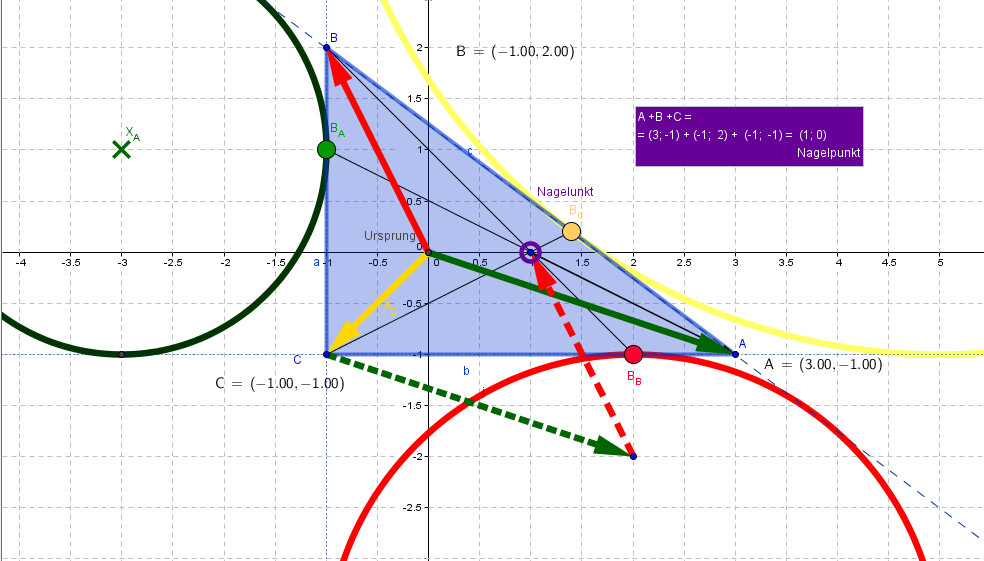
$$Nagel = A+B+C$$

Erstaunlich einfach ergibt sich der Nagelpunkt als Eckensumme $A+B+C$, wenn die Inkreismitte im Ursprung liegt! Er ist der Schnittpunkt der drei Verbindungen der Ankreis-Berührpunkte der jeweiligen drei Seiten mit den diesen gegenüberliegenden Ecken.
Die allgemeine Formel ist $$A+B+C-2\boldsymbol{M}_i$$