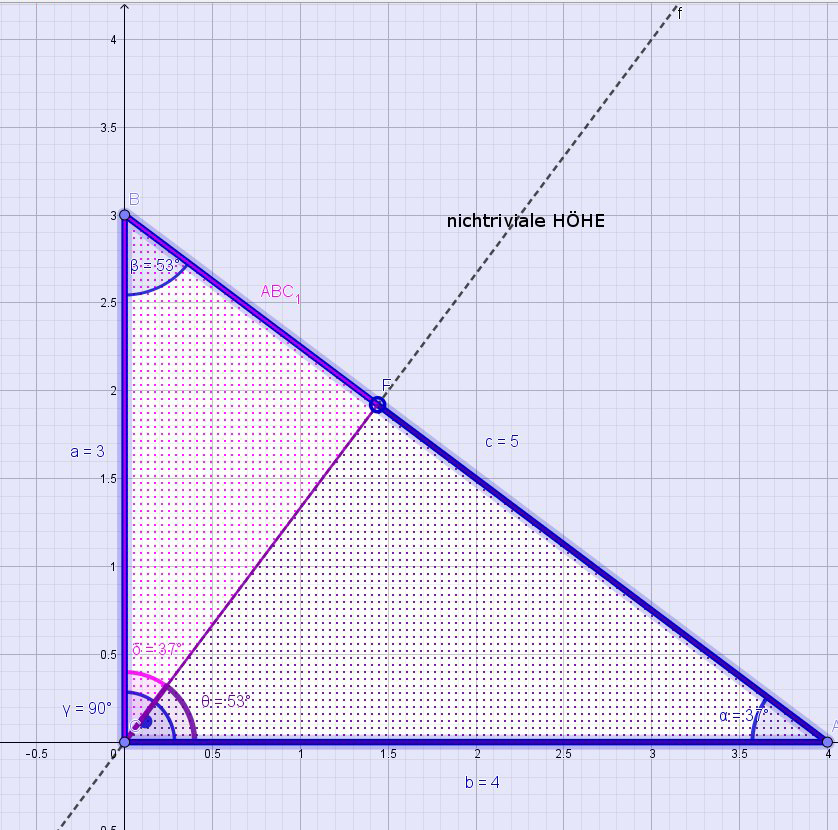
Das rechtwinklige Dreieck wird durch seine Höhe in zwei rechtwinklige Dreiecke zerlegt, die zum Ausgangsdreieck ähnlich sind, denn wenn zwei Winkel gleich sind, dann stimmen alle Winkel überein. Klappen wir nun das gesamte Dreieck um seine Hypotenuse c und die beiden Teildreiecke um die jeweils anliegende Kathete (siehe Abb.), dann gilt offensichtlich für die drei ähnlichen umgeklappten Dreiecke, dass die Flächen-Summe der beiden Katheten-Dreiecke gleich der Fläche des Hypotenusendreiecks, nämlich des Gesamtdreiecks ist! Wenn dies aber für eine von drei ähnlichen Figuren gilt (nämlich für drei ähnliche rechtwinklige Dreiecke), dann gilt es überhaupt für alle ähnlichen aufgesetzten Figuren, wie etwa für ähnliche Kaninchen (Beutelspacher). Daher gilt der Zusammenhang, (dass die Summe der beiden kleineren das größte ergibt) auch für aufgesetzte Quadrate, denn alle Quadrate sind sich ähnlich! Wer aber gerne lieber Zahlenverhältnisse mag, der berechnet die Ähnlichkeitsfaktoren der ähnlichen kleineren Teildreiecke, indem er das Verhältnis der jeweils längsten Seiten (Hypotenusen) nimmt. 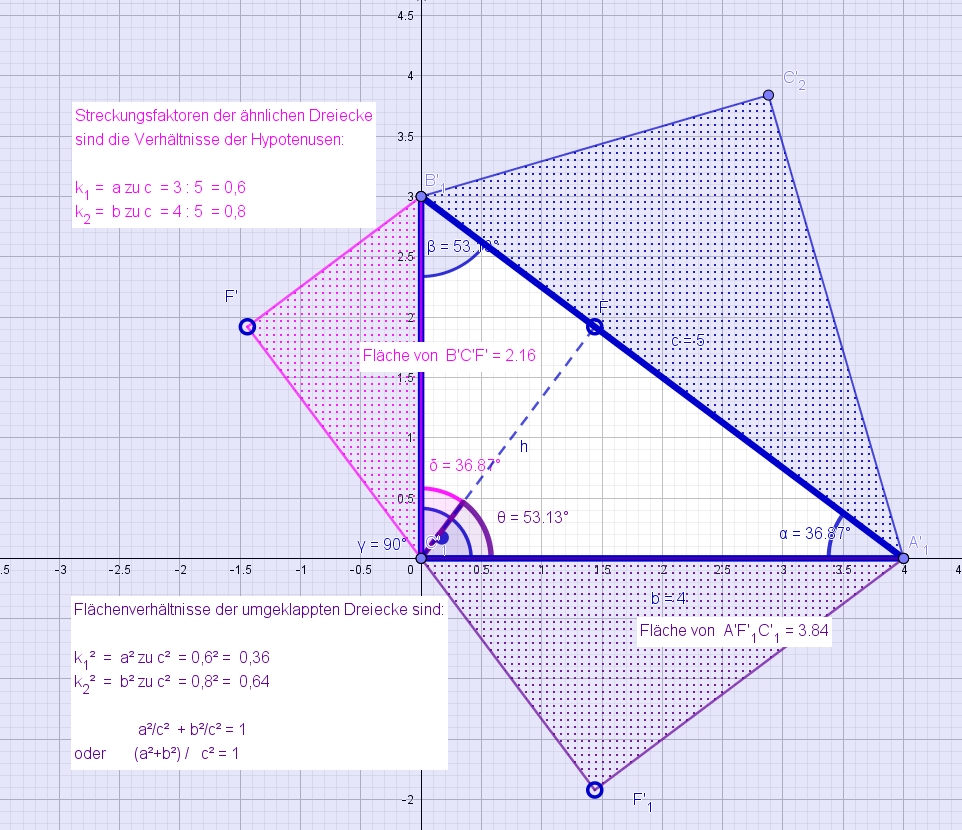Die beiden Ähnlichkeitsfaktoren $k_{1}$ und $k_{2}$ sind $a$ zu $c$ und $b$ zu $c$. Das Verhältnis der Flächen ähnlicher Figuren ist dann das Quadrat der Streckungsfaktoren, da Flächen ja das Produkt zweier Längen $(\frac{1}{2}g\cdot h)$ sind. Die Flächenverhältnisse der Kathetendreiecke zur Gesamtfläche sind $$k_{1}^{2}=\Bigl(\frac{a}{c}\Bigr)^{2}\quad also \quad A_{1}=\Bigl(\frac{a}{c}\Bigr)^2 \cdot A$$ $$k_{2}^{2}=\Bigl(\frac{b}{c}\Bigr)^{2}\quad also \quad A_{2}=\Bigl(\frac{b}{c}\Bigr)^{2} \cdot A$$ die Flächensumme ist $A$. Somit ist: $$\Bigl(\frac{a}{c}\Bigr)^{2}\cdot A + \Bigl(\frac{b}{c}\Bigr)^{2} \cdot A = A$$ oder $$\Bigl(\frac{a}{c}\Bigr)^{2} + \Bigl(\frac{b}{c}\Bigr)^{2} = 1$$ $$\frac{a^{2}+b^{2}}{c^{2}} = 1$$ $$a^{2} + b^{2} = c^{2}$$ Nun weiß man auch sofort, warum der Pythagoras nur in der Euklidischen Geometrie gilt, nämlich in einer Geometrie in der es überhaupt Ähnlichkeiten gibt. Auf der Kugeloberfläche existieren keinerlei ähnliche Figuren (rechtwinklige Dreiecke können z.B. die Winkelsumme $270°$ haben), und statt dem Pythagoras-Satz gilt ein sog. Kosinus-Satz. In allen Nichteuklidischen Geometrien gibt es keine Ähnlichkeiten und daher auch keinen Pythagoras!