Willkommen bei Udo Rehle Mathematik

τρία κοτόπουλα έξι πόδια

Drei Hennen, sechs Füße, oder anders gesagt: logisch! Aber das logische Denken scheint bei den meisten Menschen nicht so beliebt zu sein!! Auch ich selbst habe ich schon bei der Denkfaulheit ertappt, denn probieren geht über studieren! Einstein hat schon recht, wenn er sagt, daß die nur Dummheit der Menschen unendlich ist. Aber Mathematik und das Trainig logischen Schlußfolgerns sind wohl eher die Dinge, die kein Mensch gebrauchen kann. Wo braucht man denn mehr von der Logik als in der Mathematik. Bei der Chemie da haben die Elemente eben nicht nur eine Wertigkeit, sondern meist mehrere. Das ist eher schwer logisch zu verstehen. Und auch weil die Verpackung (die Elektronenhülle) wichtiger ist als der Inhalt (Kernaufbau aus Quarks), scheint eher verwunderlich. Und die an die Realität so nah anknüpfende Physik ist nicht unbedingt logisch. Bei ihr endet die Logik spätestens in der Quantenmechanik, wo es zB. einen Tunneleffekt für Teilchen gibt, die gar nicht die notwendige Energie zum Durchbrechen des Potentialwalls haben, aber dennoch tun. Aber in der Mathematik, da baut sich alles ganz logisch auf ein paar Postulaten auf. Damit ist allerdings das Wesen der Mathematik noch nicht ergründet. Das ist erst nach einer langen und andauernden Beschäftigung mit ihr zu erfahren.

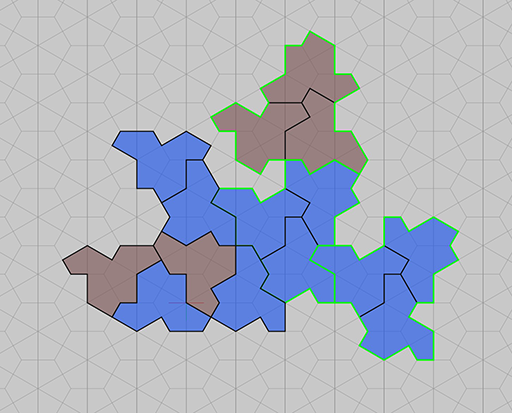
Einstein‑Kacheln

Eine einzige Form, die die Ebene aperiodisch parkettiert. Probiere es interaktiv aus.

Mehr erfahren

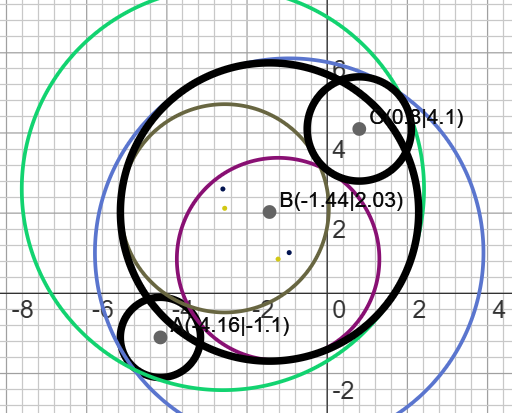
Apollonische Kreise

Bis zu acht Lösungskreise, die drei gegebene Kreise berühren – visualisiert und interaktiv.

Mehr erfahren

3D‑Viewer

Platoniche Sternkörper wie Großer Ikosaeder & Großer Dodekaeder drehen und zoomen.

Mehr erfahren

Apollonius 3D

Vier Kugeln, die die Flächen eines Tetraeders tangieren – eine räumliche Erweiterung des Klassikers.

Mehr erfahren

Kunst

Geometrische Illustrationen, Renderings und Experimente – die ästhetische Seite der Mathematik.

Mehr erfahren

Welcome to Udo Rehle Mathematics

τρία κοτόπουλα έξι πόδια

Three hens, six feet—in other words: logical! But logical thinking doesn’t seem very popular with most people!! I’ve caught myself being mentally lazy too, because practice beats theory. Einstein is right when he says that only human stupidity is infinite. But mathematics and the training of logical reasoning are apparently things nobody needs. Where would you need more logic than in mathematics?

In chemistry, elements don’t have just one valence, but usually several. That’s rather hard to understand logically. And the fact that the packaging (the electron shell) is more important than the contents (the nucleus made of quarks) seems quite surprising. And physics, which is so closely tied to reality, isn’t necessarily logical. Its logic ends at the latest in quantum mechanics, where, for example, there is a tunneling effect for particles that don’t even have the energy required to break through a potential barrier—yet do so anyway.

In mathematics, by contrast, everything is built quite logically on a few postulates. However, that still doesn’t uncover the essence of mathematics. You only come to understand that after a long and ongoing engagement with it.

Einstein Tiles

One single shape that tiles the plane aperiodically. Try it interactively.

Learn more

Apollonius Circles

Up to eight solution circles tangent to three given circles – visualized and interactive.

Learn more

3‑D Viewer

Explore stellated Platonic solids like the great icosahedron & great dodecahedron.

Learn more

Apollonius 3D

Four spheres tangent to the faces of a tetrahedron – the 3‑D extension of a classic.

Learn more

Art

Geometric illustrations, renderings and experiments – the aesthetic side of mathematics.

Learn more